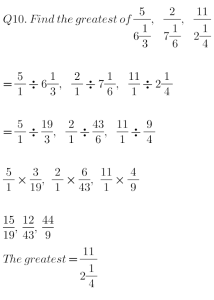FRACTIONS:
fractions are wholes that consist of Numerators and Denominators that are separated with a Division sign.
Numerator: (At the top)
Division sign: (At the middle) and
Denominator: (At the bottom).
It is simply a figure placed on another figure.
Example of a fraction is 1/x,
Where 1 is the Numerator
(/) is the division sign and
“x” is the denominator.
There are three types of fractions which are:
Proper fraction, Improper fraction and
Mixed Fraction.
Proper Fractions:
This is a fraction whose Denominator is greater than the Numerator.
Examples of Proper fraction are:
1/2, 2/3, 6/7, 6/11 etc. Provided that the numerator is lesser than the Denominator.
Improper Fractions:
Improper fraction is the one whose Numerator is greater than the Denominator. Improper fraction can further be divided to give mixed Fraction. If 11/7 is an improper fraction, it can be divided further to have a mixed Fraction of 1⁴/7. That is One whole number, four over seven.
Examples of Improper fraction are:
3/2, 4/3, 11/7, 6/5 etc. Provided that the numerator is greater than the Denominator.
Mixed Fractions:
In this type of fraction, it consists of a whole number and a proper fraction written together. Mixed Fraction is gotten from improper fraction when further divided without leaving your answer in Decimal.
Examples of Mixed fraction are 5½, 2¾, 8⅝, 3⅞ etc.
To solve problems concerning fractions is very simple if and only if the student masters and can always remember the word “BODMAS” when solving any problems involving fractions. BODMAS is an order in which arithmetic is carried out.
BODMAS = Bracket Of Division, Multiplication, Addition and Subtraction.
Example 1: Simplify 3⅔ ÷ (25¾ of 2¼ – 21)
From the BODMAS, you can see that BRACKET comes before DIVISION. So we need to clear the BRACKET first before DIVIDING. Look very well again, you will still notice that the BRACKET we are planning to clear is housing both OF and SUBTRACTION, we have to deal with OF first before SUBTRACTION because OF comes first in the word BODMAS before SUBTRACTION.

3⅔ ÷ (25¾ of 2¼ – 21) = (176)/(1773)
Example 2:
Evaluate (3¼ + 3½)/(7⅛ – 5¾)
Solution:

Example 3:
Simplify 2/3 of 5/9 x 4/7 ÷ 2/3( 5/9 + 4/7 – 2/3)
Solution: Always know the abbreviated word that comes first in the word BODMAS before others in a given Question.
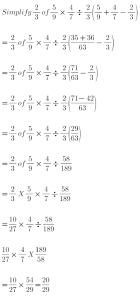
The answer to the Example 3 is = 20/29.
ORDER OF MAGNITUDE
This is the arrangement of numbers, be it whole numbers or fractions in Ascending or Descending order of their magnitudes. But in this phase, we will be discussing on how to arrange ONLY Fractions in their order of magnitude, reason is because students can not easily tell which fraction is bigger or smaller than another in a given number of fractions. It is very easy to arrange whole numbers in any order of their magnitudes.
METHODS ADOPTED TO KNOW THE MAGNITUDES OF FRACTIONS ARE TWO:
(i). Changing each and every one of the given Fractions to Decimal. That is dividing their numerators by their denominators.
(ii). Lowest common Multiple ( This is finding the L.C.M of the Fraction’s denominators and using it to multiply out each Fraction to get a whole).
Example 1:
Arrange 5/9, 2/3, 4/7, 1/3 in their ascending order of magnitude.
Solution: Using method 1
5/9 = 0.5556
2/3 = 0.6667
4/7 = 0.5714
1/3 = 0.3333
Now to arrange those Fractions in their ascending order of magnitude:
= 1/3, 5/9, 4/7, 2/3
Using method 2
Step 1: Finding the L.C.M
This is finding the L.C.M of the Fraction’s denominators.
LC.M of 3, 9 and 7 = 63
Step 2: Multiply out each Fraction with the L.C.M
5/9 x 63 = 35
2/3 x 63 = 42
4/7 x 63 = 36
1/3 x 63 = 21
Ascending order of magnitude = 1/3, 5/9, 4/7, 2/3
By now the students should be able to solve any question that comes under this topic.
QUESTIONS AND SOLUTIONS:
Q1 (a).
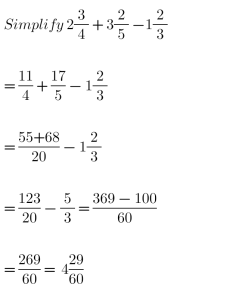
(b).
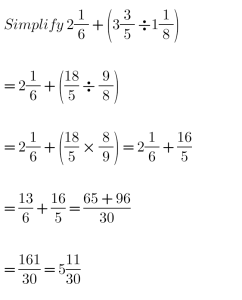
(c).
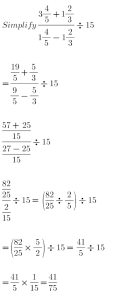
(d).
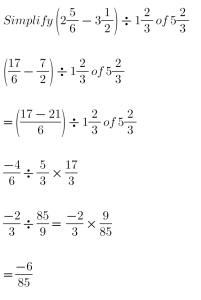
Q2(a).
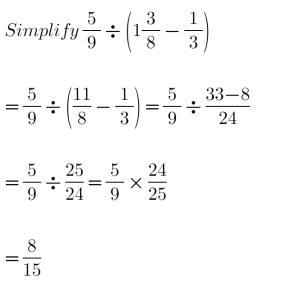
(b).
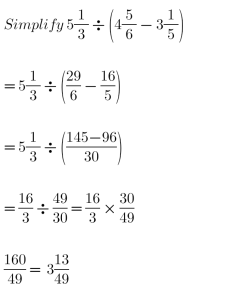
(c).
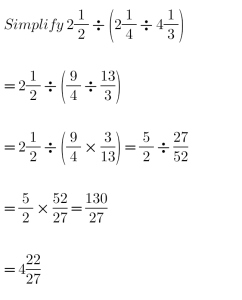
(d).
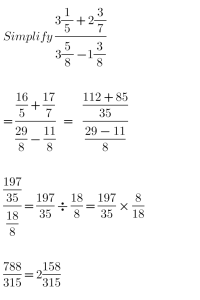
Q3. When 150 Litres has been drawn from a tank, it is ⅜ full, how many litres will the tank hold?
Solution;
Let the total litres that the tank can hold be “L” and (3/8 x L) is the remaining litres present in the tank after 150 litres has been drawn from it.
150 + (3/8 x L) = L
150 + 3L/8 = L
Try and clear the Fraction.
(8 x 150) + 3L = (8 x L)
1200 + 3L = 8L
Collect like terms
3L – 8L = – 1200
– 5L = -1200
Divide both sides by the coefficient of L
Therefore L = 240 Litres.
Q4. How many items costing 3²/5k can be bought with #85.00?
Solution:
Let the number of the items be y.
y x 3²/5k = #85.00
y x 3.40 = 85
3.40y = 85
Divide both sides by the coefficient of y.
y = 85/3.4
Therefore y = 25 items.
Q5. A man spends 5/9 of his money on rent, and 5/16 of the remainder on electricity. If the final balance remaining is #550, find how much was spent on rent.
Solution:
Let the man’s total money be “M”
Rent = 5/9 x M = 5M/9
He spent 5M/9 on Rent.
Remainder = M – 5M/9
= (9M – 5M)/9
= 4M/9
Electricity = (5/16) x (4M/9) = 20M/144
= 5M/36
He spent 5M/36 on Electricity.
Final balance after spending on both Rent and Electricity = #550
Then his total money:
M = Rent + Electricity + balance
M = 5M/9 + 5M/36 + #550
M = (20M + 5M)/36 + 550
M = 25M/36 + 550
Making all the terms to be in their Whole numbers.
36M = 25M + 19800
Collection of like terms
36M – 25M = 19800
11M = 19800
Dividing both sides by the coefficient of M.
M = (19800)/11
M = #1,800.
The man’s total money is #1,800,
The one he spent on rent is 5M/9 = 5/9 x M
= 5/9 x 1800
= #1000
Q6. Arrange the following in descending order of magnitude.
(a). 4/7, 3/5, 11/10, 14/25
Solution: Using method 1
4/7 = 0.5714
3/5 = 0.6
11/10 = 1.1
14/25 = 0.56
Now, the descending order of magnitude = 11/10, 3/5, 4/7 14/25
(b). 5/6, 11/18, 7/12, 8/9, 2/5
Solution: Using method 2
Find the L.C.M of the denominators.
Note that using either method 1 or 2 will still give you the same answer.
L.C.M of 6, 18, 12, 9 and 5 = 180
5/6 x 180 = 150
11/18 x 180 = 110
7/12 x 180 = 105
8/9 x 180 = 160
2/5 x 180 = 72
The descending order of magnitude = 8/9, 5/6, 11/18, 7/12, 2/5
Now, let us still use method 2 to prove what we are telling you.
5/6 = 0.8333
11/18 = 0.6111
7/12 = 0.5833
8/9 = 0.8889
2/5 = 0.4
Descending order of magnitude = 8/9, 5/6, 11/18, 7/12, 2/5
Have you now believed with us that either of the two methods will give you the same answer?
(c). 4/9, 11/24, 8/15, 12/20
Solution: Using Method 1
4/9 = 0.4444
11/24 = 0.4583
8/15 = 0.5333
12/20 = 0.6
Descending order = 12/20, 8/15, 11/24, 4/9
(d). 2/3, 3/4, 15/19, 10/11, 7/8
Solution:
2/3 = 0.6667
3/4 = 0.75
15/19 = 0.7895
10/11 = 0.9091
7/8 = 0.875
Descending order = 10/11, 7/8, 15/19, 3/4, 2/3
Q7. Arrange the following in descending order of magnitude.
(a). 11/13, 8/15, 6/8, 1/3
Solution:
11/13 = 0.8462
8/15 = 0.5333
6/8 = 0.75
1/3 = 0.3333
Descending order = 11/13, 6/8, 8/15, 1/3
(b). 12/17, 7/34, 2/3, 5/6
Solution:
12/17 = 0.7059
7/34 = 0.2059
2/3 = 0.6667
5/6 = 0.8333
Descending order = 5/6, 12/17, 2/3, 7/34
(c). 5/8, 5/6, 11/16, 3/4
Solution:
5/8 = 0.625
5/6 = 0.8333
11/16 = 0.6875
3/4 = 0.75
Descending order = 5/6, 3/4, 11/16, 5/8
(d). 11/15, 5/12, 19/23, 7/18
Solution:
11/15 =0.7333
5/12 = 0.4167
19/23 = 0.8261
7/18 = 0.3889
Descending order = 19/23, 11/15, 5/12, 7/18
Q8. Three men do a piece of work, the first does 7/15, the second does 5/6 of the remainder, while the third does the rest. If the rest done by the third person equals 24 units, find the whole piece of work.
Solution:
Let the work done by the three men = W
First = 7/15 x W = 7W/15
Remainder = W – (7W/15)
= (15W – 7W)/15
= 8W/15
Second man = 5/6 x (8W/15)
= 4W/9
The third = W – (7W/15 + 4W/9)
= W – (21W + 20W)/45
= W – 41W/45
= (45W – 41W)/45
The third = 4W/45 = 24 units
4W/45 = 24
Cross Multiplication will give us 4W = 1080
Dividing both sides by the coefficient of W.
W = 1080/4 = 270 pieces
Q9. Subtract the highest of 5/8, 9/11 and 3/4 from the lowest of 21/50, 13/25, 36/70
Solution:
Step 1 is to find their magnitudes.
For group A:
5/8 = 0.625
9/11 = 0.8182
3/4 = 0.75
The highest of group A = 9/11.
For group B:
21/50 = 0.42
13/25 = 0.52
36/70 = 0.5143
The lowest of group B = 21/50
Therefore, (21/50) – 9/11
= (231 – 450)/550
= -219/550
Q10.