You can only add or subtract Surds in the same basic form. Sometimes if the surds are not in the same basic form and needed to be simplified and brought to the same basic form before the addition or subtraction will be carried out.
Note:
√a + √a = 2√a
2√b – 3√b = – √b
√a + √b = √a + √b ≠ 2√ab ≠ √(a + b)
Example 1:
√2 + √2
Solution:
Since they are in the same basic form, we have to add immediately. That is √2 + √2 = 2√2
Example 2:
5√3 – √3
Solution:
5√3 – √3 = 4√3
Example 3:
√12 + 3√75
Solution:
√(4 x 3) + 3√(25 x 3)
= √(2² x 3) + 3√(5² x 3)
= 2√3 + (3 x 5)√3 = 2√3 + 15√3 = 17√3
MULTIPLICATION AND DIVISION OF SURDS
First and second RULES of Surds are applied when carrying out Multiplication and Division of Surds respectively.
First rule says that when two Surds √a and √b are multiplied (√a x √b), it is still equal to √(a x b) and also equal to √(ab)
Examples part of it:
1). √2 x √3 = √(2 x 3) = √6
2). √5 x √11 = √(5 x 11) = √55
3). 2√3 x √3 = √(2² x 3) X √3
= √(2 x 2 x 3) X √3
= √12 x √3 = √(12 x 3) = √36 = 6
Second rule says that when two Surds √a and √b are being Divided √(a/b). They can be written separately with each having it’s own root √a/√b
Examples part of it:
1). √8/√2
Solution:
Since we’re have the two Surds separate, the second rule said it is the same thing when we coat the both together provided that the Numerator and the denominator do not change their positions.
√8/√2 = √(8/2) = √4 = 2
2). √24/√3
= √(24/3) = √8 = √(4 x 2)
= √(2² x 2) = 2√2
3). √12/√4
= √(12/4) = √3
RATIONALIZATION OF SURDS
This is the process by which we remove the irrational number from the denominator of a fraction.
Here, we multiply both the numerator and the denominator of a fraction by its denominator. If the denominator is not single, we multiply the numerator and the denominator of the fraction by its denominator’s conjugate.
Note: That the conjugate of
√a + √b = √a – √b
√a – √b = √a + √b
a + √b = a – √b
a – √b = a + √b
√a + √b = – √a – √b
√a – √b = – √a + √b
Just know that in any case, it is only the sign connecting the two that will change.
Examples of Surds Rationalization.
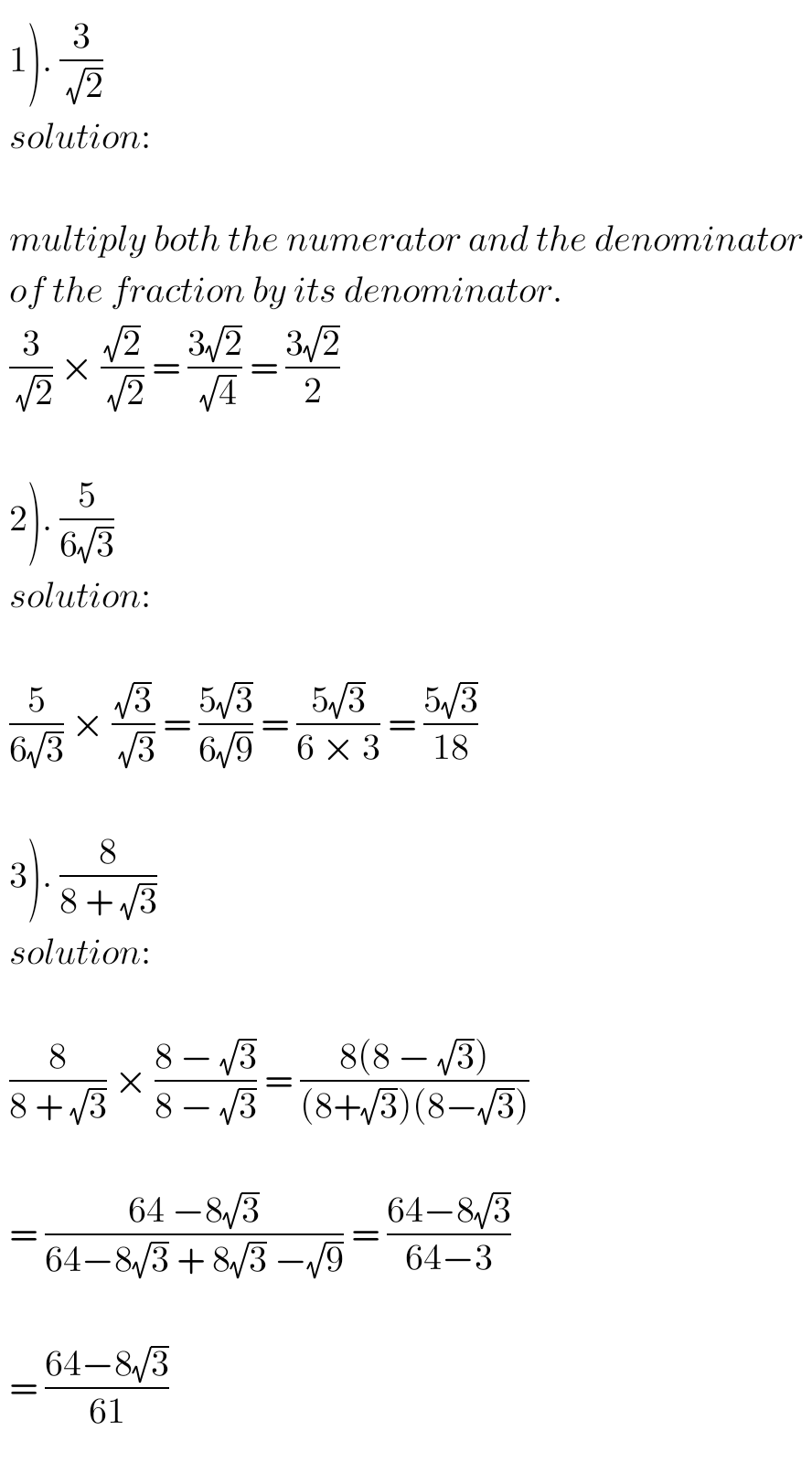
QUESTIONS AND SOLUTIONS:

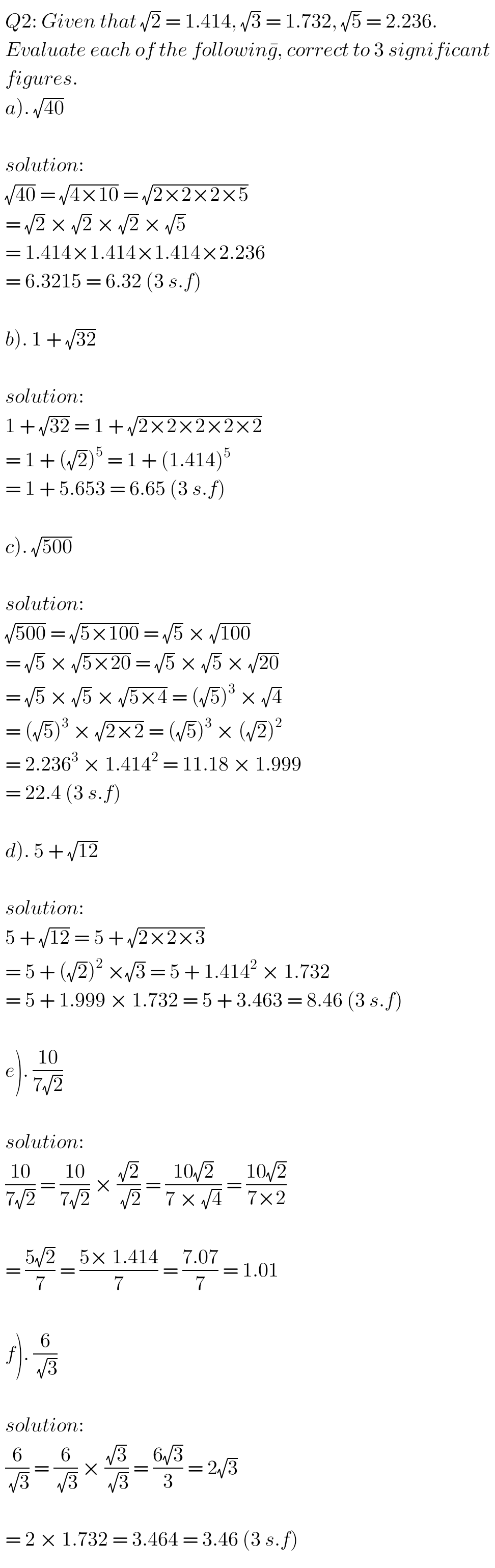
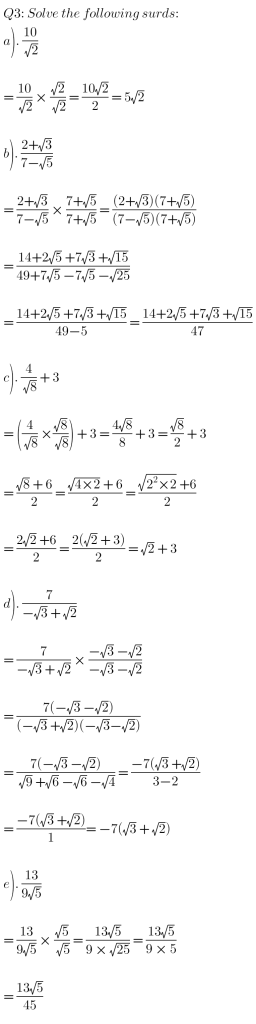
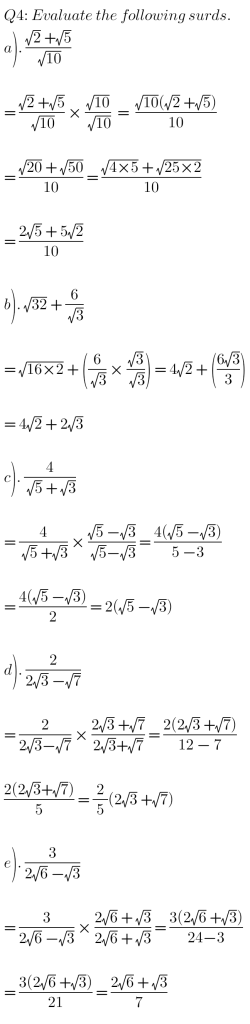
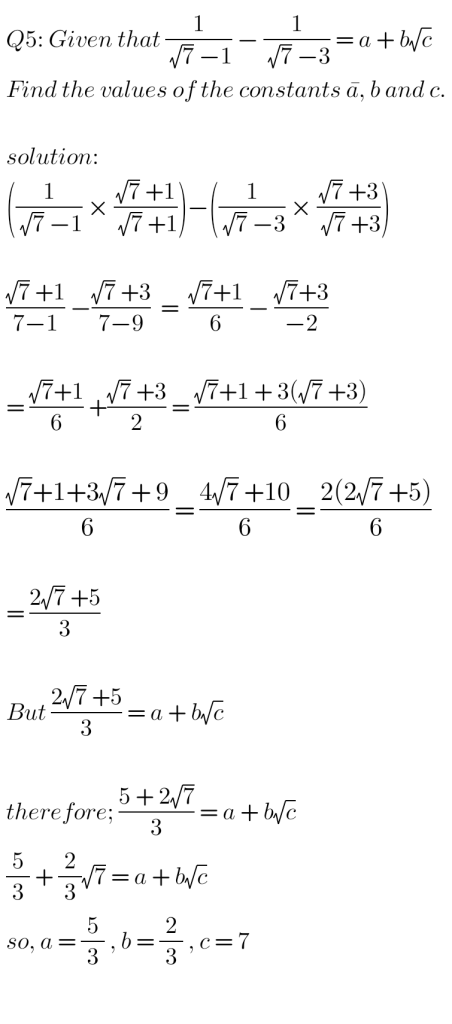
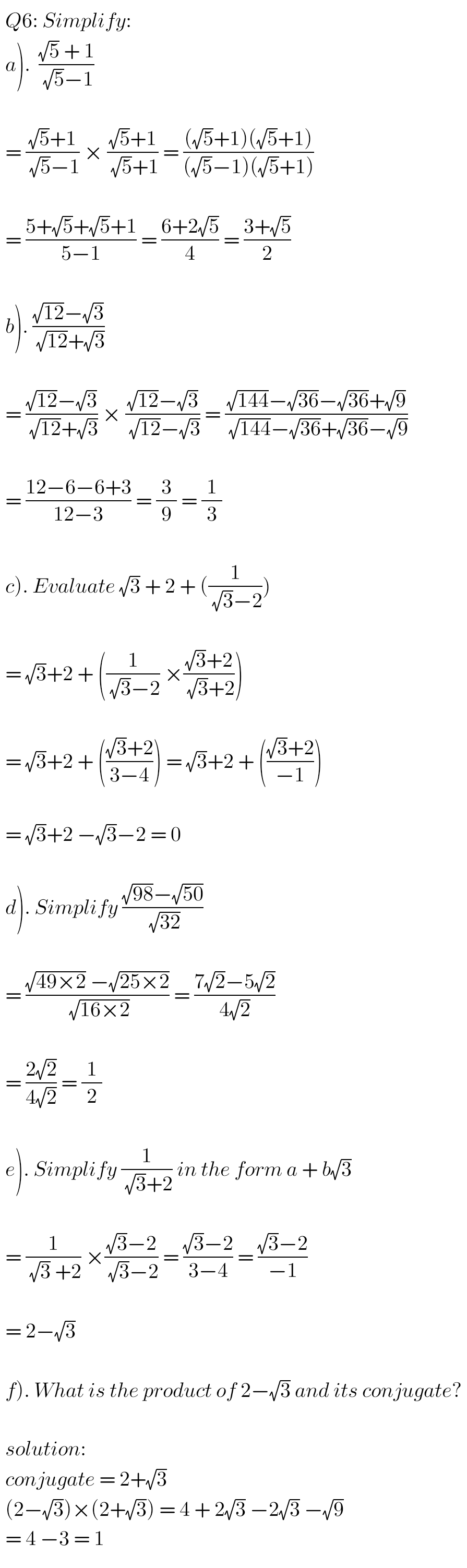
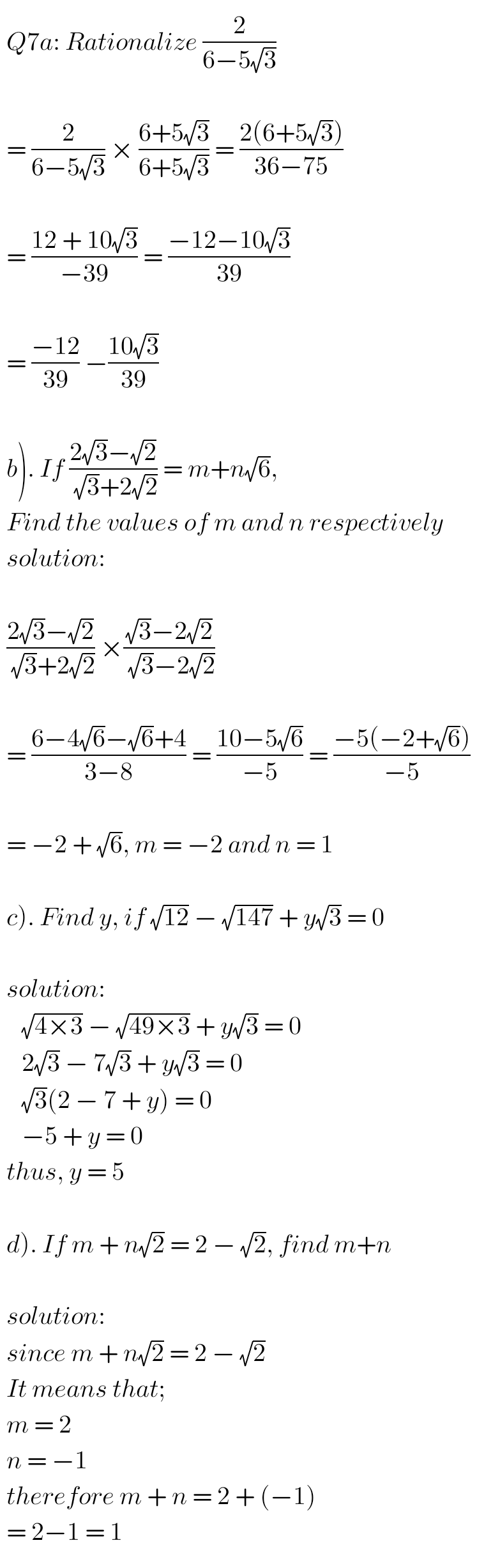
Click here to see Mathematics past questions and answers on chibase.com.ng