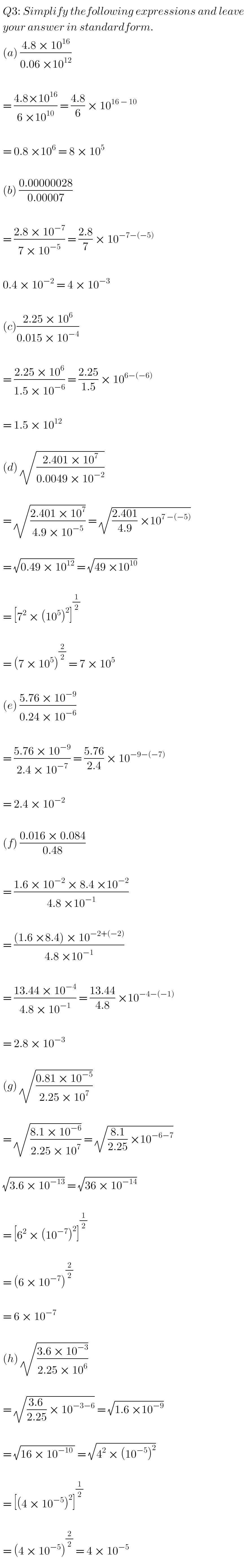Before one can add or subtract in standard form, the powers of the 10( that is ⁿ) in the numbers to be added or subtracted must be made to be equal.
Example 1:
5.4 x 10⁴ + 6.04 x 10³
Solution:
Either you make the first power to be equal to the second power or you make the second to be equal to the first.
The former:
5.4 x 10⁴ + 6.04 x 10³ = 54 x 10³ + 6.04 x 10³
= (54 + 6.04) x 10³
= 60.04 x 10³ = 6.004 x 10⁴
The latter:
5.4 x 10⁴ + 6.04 x 10³ = 5.4 x 10⁴ + 0.604 x 10⁴
= (5.4 + 0.604) x 10⁴
= 6.004 x 10⁴
Example 2:
5.32 x 106 – 3.546 x 10⁴ = 5.32 x 106 – 0.03546 x 106
= (5.32 – 0.03546) x 106
= 5.28454 x 106
MULTIPLICATION and DIVISION in standard form:
The same rule that governs the operation of indices also governs Multiplication and Division in standard form. That is, if it is Multiplication, their bases will be multiplied and their powers will be added. If it is Division, their bases will be divided and their powers will be subtracted.
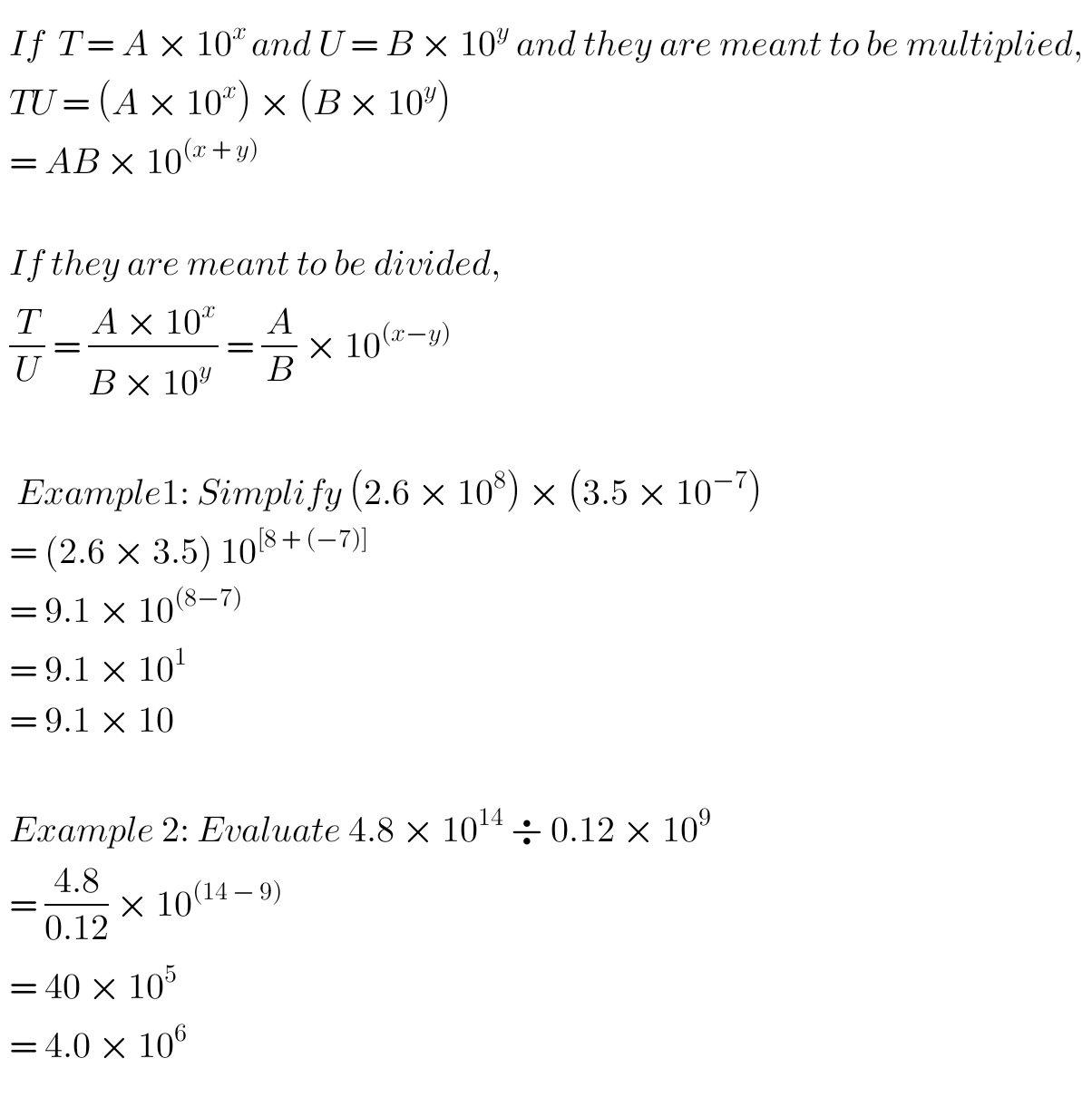
ESTIMATION
Estimation is the method of determining a rough value, quantity or anything at all by multiplying, dividing, adding or subtracting as the case may be.
Examples:
Estimate the following:
(a) 2.25 x 6.12
Solution:
Since estimation is a rough value that is not far from the real value, the estimate of the question above is
2 x 6 = 12
While the real value is 13.77 = 13.8 (to 1 d.p)
(b) 19.081 ÷ 6.609
Solution:
Estimate = 18÷ 6 = 3
Real value = 2.89 (2d.p)
(c) 45.26 + 15.06
Solution:
Estimate= 45 + 15 = 60
Real value = 60.32
(d) 58¼ – 33¾
Solution:
Estimate = 58 – 33 = 25
Real value = 24½
QUESTIONS AND SOLUTIONS:
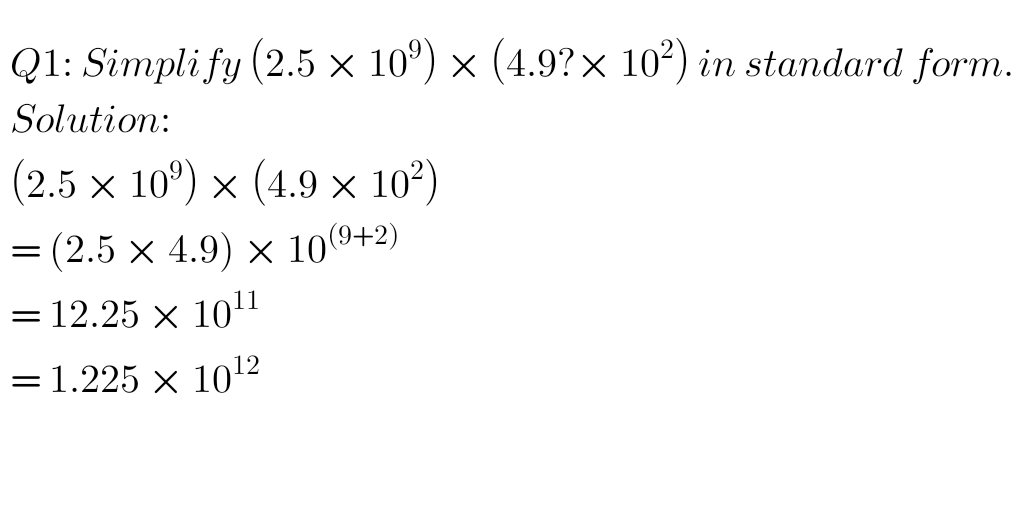
Question 1 and its Solution