Log Number: We are going to look into the use of logarithm of numbers in this very Article.
The logarithm of a number (let’s say “N”) to a particular base (let’s say “b”) is that power/index to which “b” MUST be raised to give us “N”.
Good knowledge of standard form will help a student when dealing with logarithm of a number.
Logarithm of numbers greater than 1
Logarithm of numbers greater than 1 has both characteristic and Mantissa , the Characteristic is gotten/known by either Standard form or by inspection while the Mantissa is found by using four figure table.
To find the logarithm of a number to base 10, there are two key definitions and they are crucial. They are CHARACTERISTICS and MANTISSA.
- Characteristics of a logarithm: This is the integral/whole number part of a logarithm. The characteristics is always one (1) less than the number of digits in the integral part.
Examples of Numbers greater than 1 and their Characteristics
| Numbers greater than 1 | Their Characteristics |
| 10 | 1 |
| 100 | 2 |
| 875 | 2 |
| 1000 | 3 |
| 34.26 | 1 |
| 3426 | 3 |
| 342.6 | 2 |
Example 1, for logarithm of 10000:
Using standard form, 10000 = 1.0000 x 10⁴
Thus the Characteristic = 4. (this is because the number of digits in the integral/whole number part of the logarithm is five and must be one less than the total digits)
- Mantissa of a logarithm: This is the decimal part of a logarithm and it is found using four figure tables to four decimal of places.
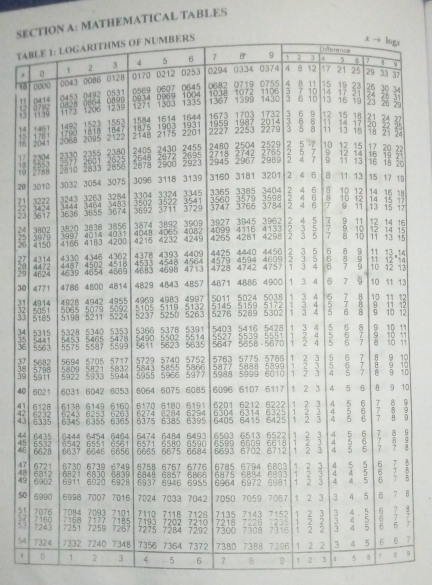

From example 1 above: To find the Mantissa of 1.0000 using your four figure table.
Note that the Characteristic of 10000 = 4.
Mantissa: look for 10 under 0 and difference 0
10 under 0 = 0000
Difference 0 = (logarithm of numbers doesn’t have difference zero)
Therefore, Log 10000 = 4.000
When a number is divided or multiplied by a power of 10, the Mantissa will not change but the Characteristics will change.
Example 2: Find the logarithm of 4387
Solution:
First step is to know the Characteristic of that log number by either Standard form or by inspection.
By standard form: 4387 = 4.387 x 10³, Characteristic = 3.
By Inspection: From what we discussed above, we said that the Characteristic of a logarithm is always one less than the number of digits in the whole number part, number of digits in 4387 = 4, which means that 3 is the characteristic because it is one lesser than four.
Second step is to find the Mantissa of 4.387 by using the four figure table.
43 under 8 = 6415
Difference 7 = 7
Adding the two will give us 6422
Therefore the logarithm of 4387 = 3.642
Example 3: Find the logarithm of 6.243
Solution:
Characteristic by standard form 6.243 = 6.243 x 10°
Thus the Characteristic = 0.
Look for the Mantissa
62 under 4 = 7954
Difference 3 = 2
Add both = 7956
Therefore Log 6.243 = 0.7956
Example 4: Find the logarithm of 62.43
Solution:
Characteristic by inspection = 1.
Look for the Mantissa
62 under 4 = 7954
Difference 3 = 2
Adding both = 7956
Thus, Log 62.43 = 1.7956
Logarithms of Numbers less than 1
To evaluate the logarithm of numbers less than 1 from the four figure table, it differs only by its characteristic. The Characteristic has a negative sign. We represent it by crossing a Bar over the characteristic.
Note also that the Characteristic of log number less than 1 depends on the number of zeros counting from the left to the first significant figure.
If a Characteristic of a log number is -3., it is pronounced Bar 3 and should be written this way below:

The reason why it is written like that is because it affects only the Characteristics while the Mantissas remain unchanged.
Examples of Numbers less than 1, their Standard forms and Characteristics
| Numbers less than 1 | Their Standard forms | Characteristics |
| 0.923 | 9.23 x 10-1 | -1 |
| 0.0923 | 9.23 x 10-2 | -2 |
| 0.00923 | 9.23 x 10-3 | -3 |
| 0.000923 | 9.23 x 10-4 | -4 |
Example 5: Find the logarithm of 0.4356
Solution:
The Characteristic either by standard form or by inspection is -1.
For the Mantissa:
43 under 5 = 6385
Difference 6 = 6
Add both = 6391

Students can solve any questions on logarithm of numbers once they understand how to get both the characteristic and the Mantissa of a logarithm.
QUESTIONS AND SOLUTIONS (log number)
Using the table, find the logarithms of the following numbers.
Q1: 6935
Solution:
Characteristic by standard form 6935 = 6.935 x 10³ = 3.
Mantissa:
69 under 3 = 8407
Difference 5 = 3
Add both = 8410
Thus, Log 6935 = 3.8410
Q2: 8361
Solution:
Characteristic = 3.
Mantissa:
83 under 6 and difference 1 = 9223
So, Log 8361 = 3.9223
Q3: 709
Solution:
Characteristic = 2.
70 under 9 and difference 0 = 8506
Therefore Log 709 = 2.8506
Q4: 376.4
Solution:
The Characteristic = 2.
37 under 6 and difference 4 = 5757
Thus, Log 376.4 = 2.5757
Q5: 29.41
Solution:
The Characteristic = 1.
29 under 4 and difference 1 = 4684
Log 29.41 = 1.4684
Q6: 63.2
Solution:
Characteristic = 1.
63 under 2 = 8007
:- Log 63.2 = 1.8007
Q7: 6.247
Solution:
The Characteristic = 0.
62 under 4 and difference 7 = 7957
Log 6.247 = 0.7957
Q8: 0.4269
Solution:

42 under 6 and difference 9 = 6303

Q9: 0.0986
Solution:
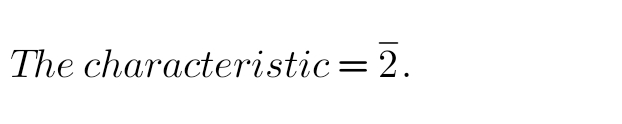
98 under 6 = 9939
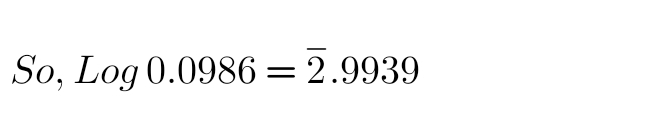
Q10: 0.00064
Solution:
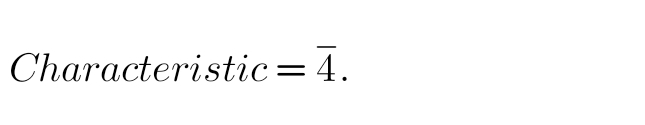
64 under 0 = 8062
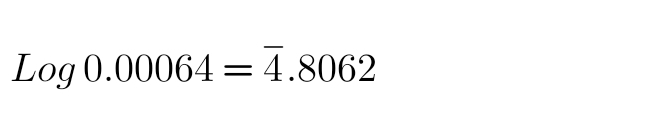
Q11: 26.09
Solution:
The Characteristic = 1.
26 under 0 and difference 9 = 4165
Log 26.09 = 1.4165
Q12: 396.5
Solution:
Characteristic = 2.
39 under 6 and difference 5 = 5982
Therefore Log 396.5 = 2.5982
Q13: 3.042
Solution:
The Characteristic = 0.
30 under 4 and difference 2 = 4832
Log 3.042 = 0.4832
Q14: 9.006
Solution:
Characteristic = 0.
90 under 0 and difference 6 = 9545
Log 9.006 = 0.9545
Q15: 0.0604
Solution:
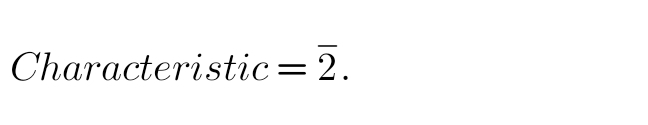
60 under 4 = 7810
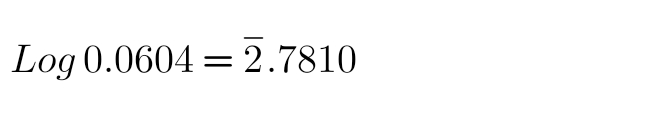
Q16: 63.24
Solution:
The Characteristic = 1.
63 under 2 and difference 4 = 8010
Therefore Log 63.24 = 1.8010
Q17: 6.324
Solution:
The Characteristic = 0.
63 under 2 and difference 4 = 8010
Thus, Log 6.324 = 0.8010
Q18: 632.4
Solution:
The Characteristic = 2.
63 under 2 and difference 4 = 8010
Log 632.4 = 2.8010
Q19: 6324
Solution:
Characteristic = 3.
63 under 2 and difference 4 = 8010
Log 6324 = 3.801p
Q20: 69.35
Solution:
Characteristic = 1.
69 under 3 and difference 5 = 8410
Log 69.35 = 1.8410
Click here and learn how to find Anti Logarithm of numbers
Always visit intellectsolver.com for new updates.
Click here to see Mathematics past questions and answers on chibase.com.ng