Operations with Surds
Whenever they talk about Surds, just bear it in mind they are directly talking about irrational numbers which can not be expressed as fraction. The reason why Surds are irrational numbers is because their exact values can not be determined. The square root of all non perfect squares are irrational, π and e are also irrational numbers because it is only their approximate values that can be known.
We can not discuss IRRATIONAL NUMBERS without also telling you what RATIONAL NUMBER is: Rational number is expressed as the Ratio of two integers x/y, where the denominator “y” is not equal to Zero (y ≠ 0).
Examples of Rational numbers are 5, ¾, ⅔, 2.5, 3/2, etc.
In other words, Surds are the ROOTS of rational numbers whose values can not be expressed as exact fractions. Examples of Surds are ✓2, ✓3, ✓5, ✓7, √11, ✓13 and so on.
RULES OF SURDS
There are four basic rules of Surds mostly used when carrying out operations on Surds.
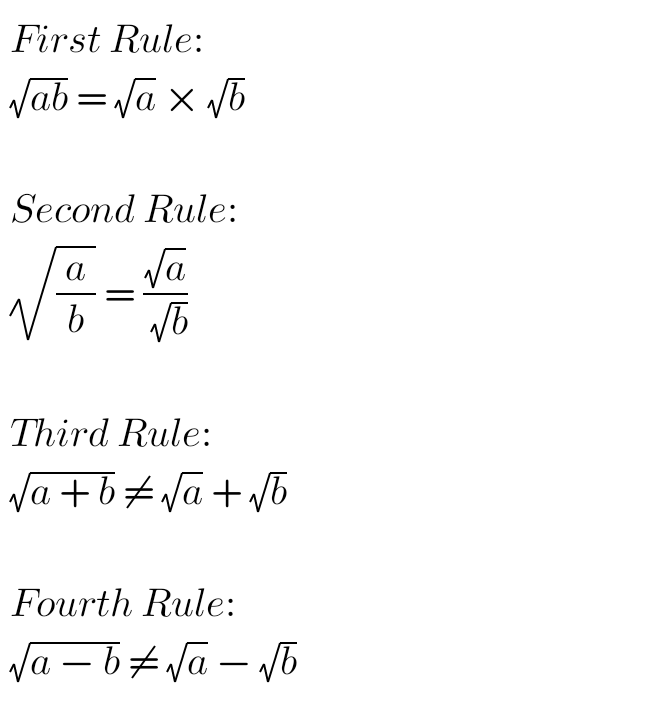
Provided that both “a” and “b” are positive.
BASIC FORMS OF SURDS
If “a” doesn’t have a factor that is a perfect square, ✓a is said to be in its basic form.
Examples of Surds that are in their basics forms are: √2, √3, √5, √6, √7, √10, √11, √13 and so on; reason, is because they can not be broken down further into two factors where one of the factors is a perfect square.
Examples of Surds that are NOT in their basics forms and needed to be in their basics forms are:
i) √8
We can break it down and have two factors, where one is a perfect square root. √8 = √(4 x 2) = √4 x √2 = 2 x √2 = 2√2.
So, 2√2 is now in its basic form.
ii) √18
Breaking it down will give us √(9 x 2) = √9 x √2 = 3√2
SIMILAR SURDS
Surds are said to be similar if their irrational parts are the same. Examples of similar Surds are:
I) 4√x and 2√x
√x = √x
ii) 3√n and 7√n
√n = √n
III) 5√y and 3√y
√y = √y
iv) 2√b and 3√b
√b = √b
NON SIMILAR SURDS
I) 4√x and 2√n
√x ≠ √n
ii) 3√y and 7√n
√y ≠ √n
III) 5√y and 3√b
√y ≠ √b
iv) 2√x and 3√b
√x ≠ √b
CONJUGATE SURDS
Conjugate surds are two different surds whose product results in a rational number.
(a + b)(a – b) = a² – b²
Similarly
(√a + √b)(√a – √b)
= (√a)² – (√b)² = a – b
Just note that the conjugate of
I) √a – √b = √a + √b
ii) √a + √b = √a – √b
SIMPLIFICATION OF SURDS
When simplifying surds, it can be done in two methods, either in their simplest form or as a single surd.
Examples: simplify the following in their simplest form.
a) √27
Solution:
√27 = √9 x √3 = 3√3
b) √75
Solution:
√75 = √25 x √3 = 5√3
Simplify (a) 2√5, (b) 3√2, (c) 11√7 as a single surd:
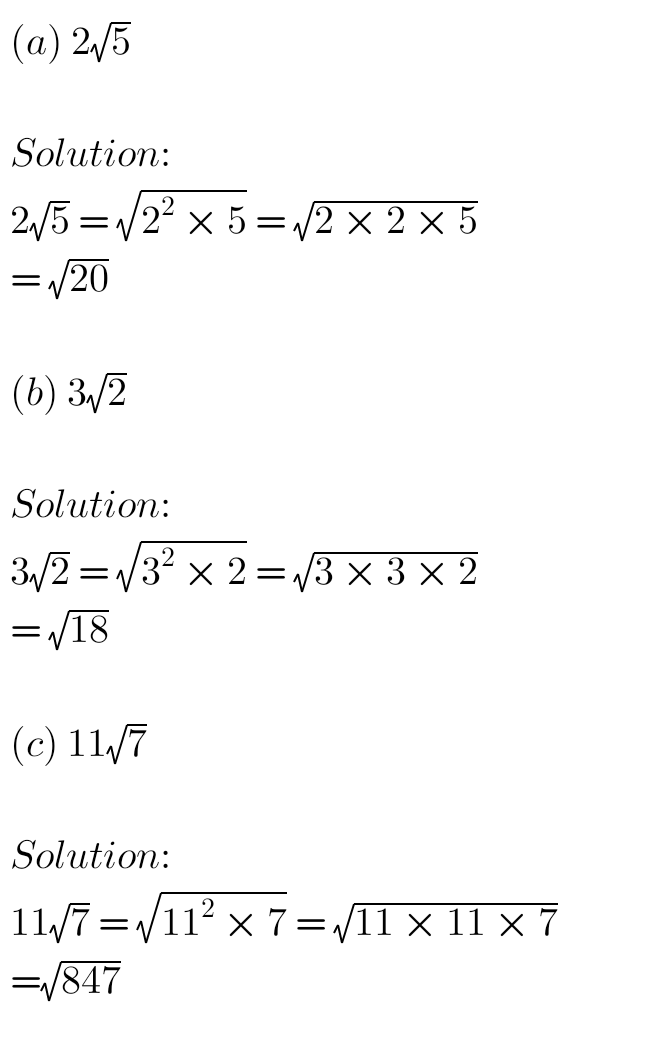
QUESTIONS AND SOLUTIONS (Operations with Surds)
Q1: Simplify the following:
(a) √8, (b) √60, (c) √240, (d) √98, (e) √200, (f) √50, (g) √72, (h) √150
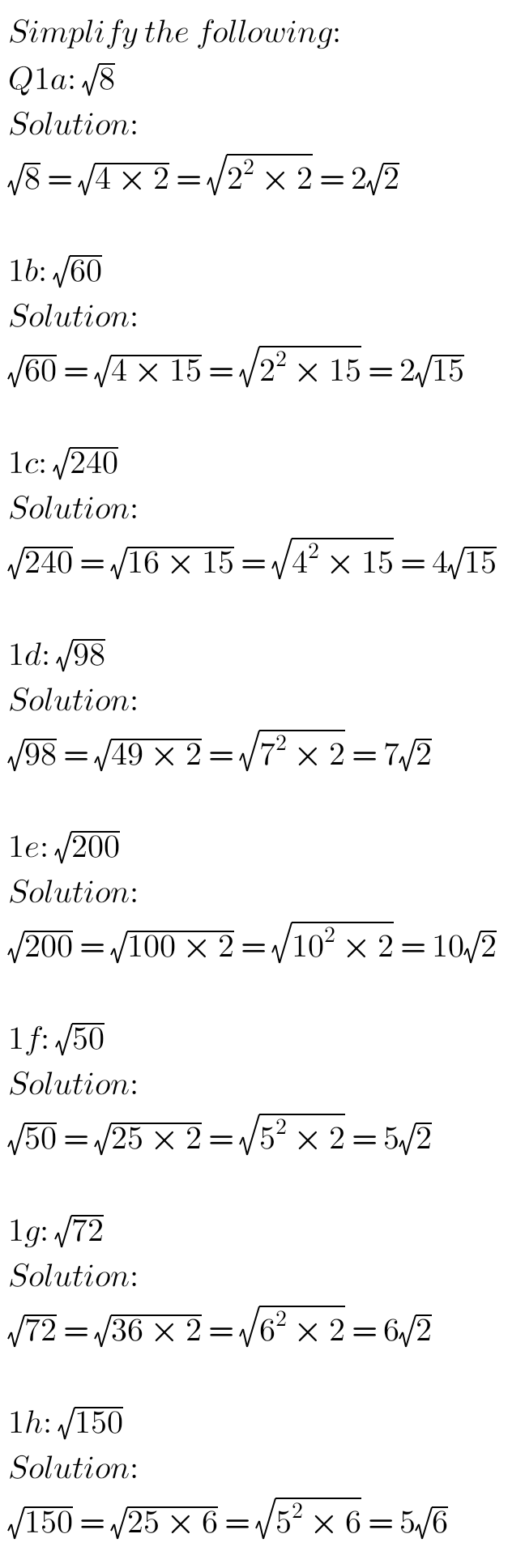
Q2: Express in single Surds:
(a) 2√10, (b) 5√3, (c) 4√3, (d) 3√7, (e) 4√11, (f) 13√7, (g) 7√6 (h) 11√6

Click here to see Mathematics past questions and answers on chibase.com.ng