The Reciprocal of any given number “x” is 1(one) all over that particular given number “x” = 1/x. (Reciprocals of Numbers)
When two numerals multiply themselves and the product is 1, the two numerals are said to be reciprocals of each other.
If a numeral is represented with the letter N, and N is not equal to Zero (N ≠ 0), then 1/N is the Reciprocal of N and vice versa.
For example if we multiply 8 by ⅛, you will see that the product is 1, therefore the reciprocal of 8 is ⅛ and also the reciprocal of ⅛ is 8.
Reciprocal Table
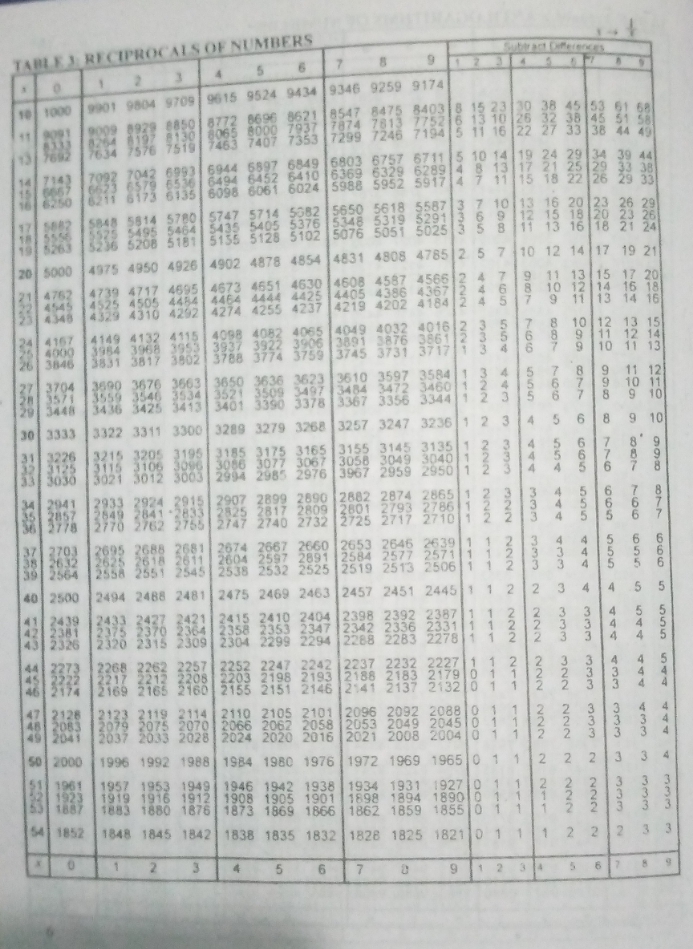

The Reciprocal table on a norm gives the reciprocals of numbers between 10 and 100. Other reciprocals such as the ones with decimal points are found the way squares and square roots tables are done.
How to find the reciprocals of any given number.
Example 1:
If for instance we are given 66.28 to find its reciprocal.
First step: Is to open where Reciprocals of numbers is written on your four figure table.
Second step: Is to look for 66 under 2 and difference 8.
66 under 2 = 1511
Difference 8 = 2
Now subtract the difference from 1511 = 1511- 2 = 1509 which is the number required. Now, estimating the correct value of the Reciprocal of 66.28.
Remember we said earlier that the Reciprocal of any given number is 1(one) all over that particular given number.
So the Reciprocal of 66.28 is 1/66.28, which lies between 1/65 and 1/70 which is 0.01538 and 0.01429.
So from the value of 1509 gotten from the reciprocal table, thus the reciprocal of 66.28 = 1/66.28 = 0.01509
Example 2:
Find the reciprocal of 662.8
Solution:
66 under 2 and difference 8 in example 1 gives 1509.
To estimate the correct value: 1/662.8 lies between 1/650 and 1/700, that is between 0.001538 and 0.001429, then the correct value of 1/662.8 = 0.001509.
Example 3:
Find the reciprocal of 6628
Solution:
66 under 2 and difference 8 when evaluated in example 1 gives 1509.
Now, estimating the correct value: 1/6628 lies between 1/6500 and 1/7000, that is between 0.0001538 and 0.0001429, therefore the correct value of 1/6628 = 0.0001509.
Example 4:
Evaluate 1/0.03349
Solution:
Look for 33 under 4 = 2994
Difference 9 = 8
Subtract 8 from 2994 = 2986
1/0.03349 lies between 1/0.03 and 1/0.035 which is between 33 and 28.
Thus, 1/0.03349 = 29.86
We all should know that the smaller the denominator, the bigger the reciprocal and the bigger the denominator, the smaller the reciprocal.
QUESTIONS AND SOLUTIONS (Reciprocals of Numbers)
Q1: Evaluate the reciprocals of the following figures from the table.
a). 69
Solution:
Look for 69 under 0 = 1449.
The correct value of the reciprocal of 69 which is 1/69 lies between 1/65 and 1/70, that is between 0.01538 and 0.01429.
The value of 1449 we got from the table, 1/69 is therefore 0.01449
b) 8.92
Solution:
89 under 2 = 1121
The correct value of 1/8.92 lies between 1/85 and 1/90 which is between 0.01176 = 0.1176 and 0.01111 = 0.1111
The value of 1121 gotten from the four figure table, 1/8.92 is therefore 0.1121
c) 6.728
Look for 67 under 2 = 1488
Difference 8 = 2
Subtracting the difference from 1488 = 1486
Correct value of 1/6.728 lies between 1/65 and 1/70 which is between 0.01538 = 0.1538 and 0.01429 = 0.1429
The value of 1486 gotten from the four figure table, 1/6.728 is therefore 0.1486
d) 0.003461
Solution:
34 under 6 = 2890
difference 1 = 1.
2890 – 1 = 2889
Estimating the correct value: 1/0.003461 lies between 1/0.003 and 1/0.0035, that is between 333 and 285, therefore the correct value of 1/0.003461 = 288.9
e) 0.0027
Solution:
Without wasting time, let’s solve straight since we all have already known the procedures.
27 under 0 = 3704
The correct value of 1/0.0027 lies between 1/0.0025 and 1/0.003, which is between 400 and 333
So the correct value of 1/0.0027 = 370.4
f) 0.2496
Solution:
24 under 9 = 4016
Difference 6 = 10
4016 – 10 = 4006
Correct value of 1/0.2496 lies between 1/0.2 and 1/0.25, which is between 5 and 4
So, the correct value of 1/0.2496 = 4.006
g) 12.93
Solution:
12 under 9 = 7752
Difference 3 = 10
7752 – 10 = 7742
True value of 1/12.93 lies between 1/10 and 1/15, which is between 0.1 and 0.06
The correct value of 1/12.93 = 0.0773
h) 2496
Solution:
24 under 9 = 4016
Difference 6 = 10
4016 – 10 = 4006
The correct value of 1/2496 lies between 1/2000 and 1/2500 which is 0.0005 and 0.0004
The true value of 1/2496 = 0.0004006
Q2: Estimate the following:
a) 2.7 + (1/2.7)
Solution:
2.7 + 1/2.7
2.7 + 0.3704 = 3.0704
b) (√66.94) + [1/(3.4)²]
Solution:
Use the method of estimating square roots of numbers to find (√66.94)= 8.181
Use the method of estimating square of numbers to find (3.4)² = 11.56 and 1/(3.4)² = 0.08651
(√66.94) + [1/(3.4)²] = 8.181 + 0.08651 = 8.268
c) 150/(6.249)²
Solution:
Using the method of estimating square of numbers to find (6.249)² = 39.05
So, 150/(6.249)² = 150/39.05 = 3.841
d) 1/0.0638
Solution:
Check 63 under 8 = 1567
The correct value of 1/0.0638 lies between 1/0.06 and 1/0.07 which is between 16 and 14
So the correct value is 15.67
Q3: Arrange the following in descending order of magnitude:
⅓, 0.4, 1/7, 1/0.2, (√3.61)
Solution:
0.4 = 2/5, 1/0.2 = 5, (√3.61) = 1.9 = 19/10
⅓, 2/5, 1/7, 5, 19/10
Multiply each of the terms with the LCM of their denominators 270.
⅓ x 210, 2/5 x 210, 1/7 x 210, 5 x 210, 19/10 x 210
70, 84, 30, 1050, 399
Therefore the descending order of magnitude = 1050, 399, 84, 70, 30
= 1/0.2, (√3.61), 0.4, ⅓, 1/7
Q4: Given that 1/p = 1/q + 1/r, find the value of p if q = 60 and r = 35.
Solution:
1/p = 1/60 + 1/35
1/p = 19/420
19p = 420
p = 420/19 = 22.11
Q5: Simplify [√(1/0.678) + (1/0.00372)]
Solution:
Using method to find Square roots of numbers [√(1/0.678) + (1/0.00372)]
√(1.479 + 268.8) = ✓270.3 = 16.44
Click here to see Mathematics past questions and answers on chibase.com.ng