
ADDITION AND SUBTRACTION IN NUMBER BASES.
Most students have been finding it so difficult to add or subtract in number bases. The method used on tackling the problems is not different from what we have done here.
Example 1: (Number Bases)
If you are given 264, 86, 475 all in base nine to be added.
Do not hesitate to convert those numbers first to base ten.
For 264nine
= 2 x 9² + 6 x 9¹ + 4 x 9° = 162 + 54 + 4
= 220ten
For 86nine
= 8 x 9¹ + 6 x 9° = 72 + 6
= 78ten
For 475nine
= 4 x 9² + 7 x 9¹ + 5 x 9° = 324 + 63 + 5
= 392ten
Step two: Add up all those numbers in base ten.
220 + 78 + 392 = 690ten.
Final step is to convert it back to base nine.
Learn how to convert from base ten to any required base here.
Therefore, (264 + 86 + 475)nine
= 846nine.
Example 2. (Number Bases)
Subtract 265 from 317 in base eight.
Solution:
First convert to base ten.
For 265eight
= 2 x 8² + 6 x 8¹ + 5 x 8° = 128 + 48 + 5
= 181ten
For 317eight
= 3 x 8² + 1 x 8¹ + 7 x ° = 192 x 8 x 7
= 207ten
Step two: Now subtract
207 – 181 = 26ten.
Final step is to convert it back to base eight.
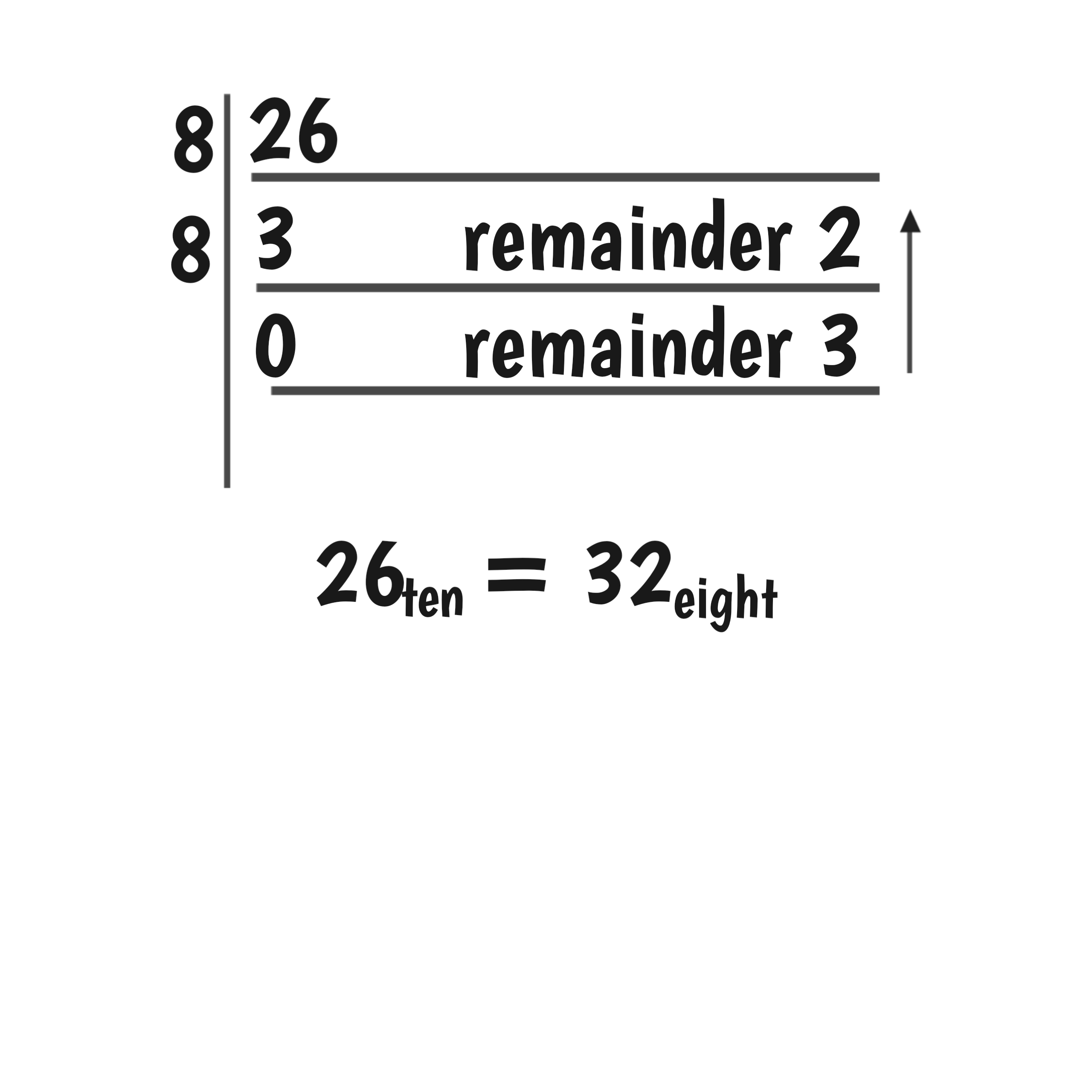
Thus, (317 – 265)eight = 32eight.
Example 3. (Number Bases)
If 123 + 1302 + xxxx in base four is 10122four, find the missing figure.
Solution:
First convert the known figures to base ten.
For 123four
= 1 x 4² + 2 x 4¹ + 3 x 4° = 16 + 8 + 3
= 27ten
For 1302four
= 1 x 4³ + 3 x 4² + 0 x 4¹ + 2 x 4°
= 64 + 48 + 0 + 2
= 114ten
For 10122four
= 1 x 4⁴ + 0 x 4³ + 1 x 4² + 2 x 4¹ + 2 x 4°
= 256 + 0 + 16 + 8 + 2
= 282ten
Step 2: Subtract (27 + 114)ten from 282ten
= 282 – 141 = 141ten
Step 3: Convert the 141ten back to the required base .

Therefore, xxxx = 2031.
MULTIPLICATION AND DIVISION OF NUMBER BASES
This is not different from the one we have done when adding or subtracting number bases. As far as you know what multiplication, division, addition and subtraction are all about. All you have to do first is to convert to base ten, then return the answer gotten to the required base.
Example 1: (Number Bases)
Evaluate 321six X 25six
Solution:
Step 1: Convert to base ten first.
For 321six
= 3 x 6² + 2 x 6¹ + 1 x 6°
= 108 + 12 + 1
= 121ten
For 25six
= 2 x 6¹ + 5 x 6°
= 12 + 5
= 17ten
Step 2: Multiply 121 by 17
= 121 x 17
= 2057ten
Step 3: Convert back to base six

321six X 25six = 13305six.
Example 2: (Number Bases)
Find the product of 1011two and 1101two.
Solution:
Step 1: Convert to base ten
For 1011two
= 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2°
= 8 + 0 + 2 + 1
= 11ten
For 1101two
= 1 x 2³ + 1 x 2² + 0 x 2¹ + 1 x 2°
= 8 + 4 + 0 + 1
= 13ten
Step 2: Multiply the two.
11 x 13 = 143ten
Step 3: Convert it back to base two.

1011two X 1101two = 10001111two
Example 3:
If 231 base four X 10101 base two = “M” base six, Find M.
Solution:
Do you notice that they are of different bases?. Do not panic because you can still solve it😊😊
Step1: Convert the two numbers to base ten
For 231 base four
= 2 x 4² + 3 x 4¹ + 1 x 4°
= 32 + 12 + 1
= 45 base ten
For 10101 base two
= 1 x 2⁴ + 0 x 2³ + 1 x 2² + 0 x 2¹ + 1 x 2°
= 16 + 0 + 4 + 0 + 1
= 21 base ten
Step 2: Multiply the two.
45 x 21 = 945 base ten
Step 3: Convert to the required base.
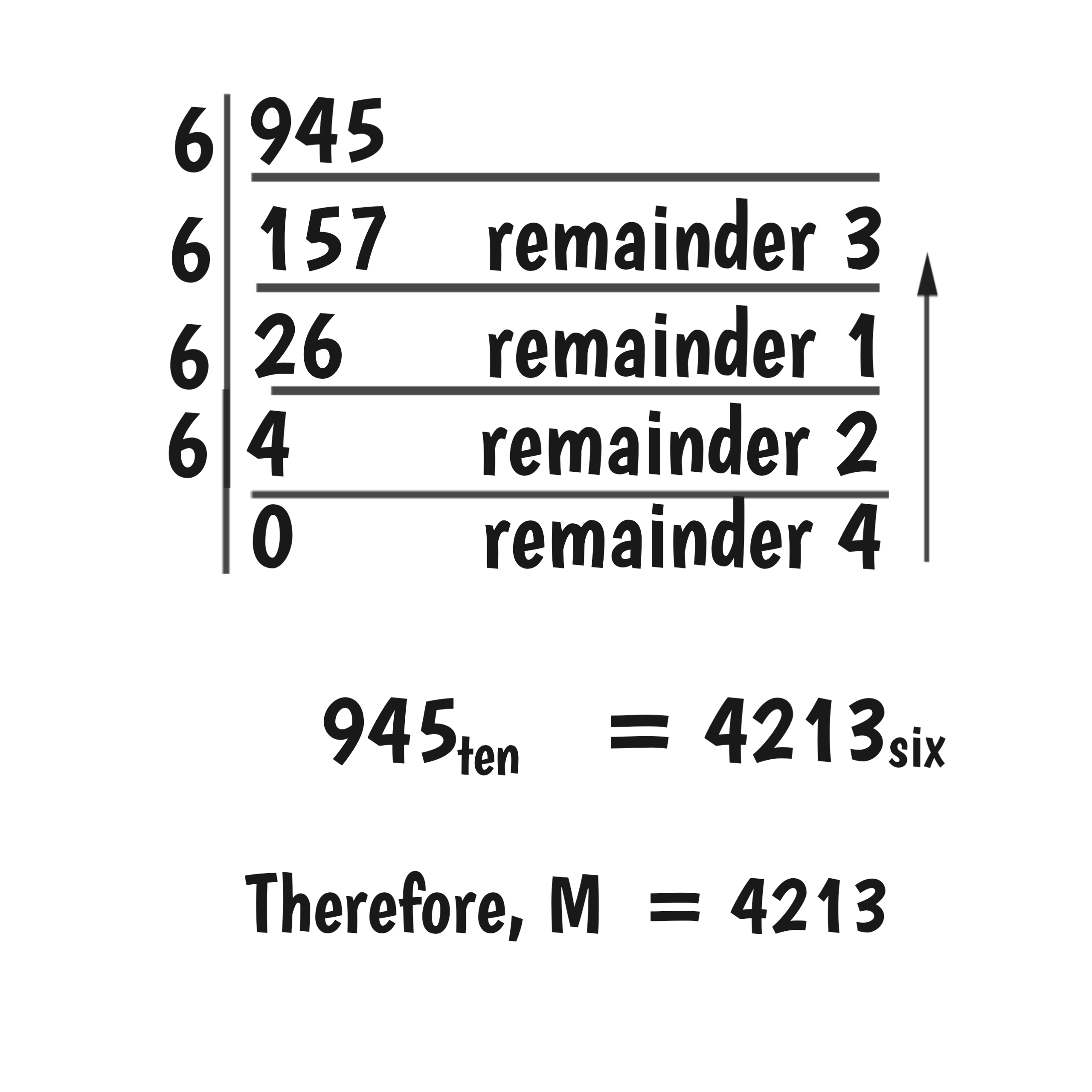
231 base four X 10101 base two = 4213 base six
Therefore, M = 4213
Example 4:
Evaluate 2115 base seven ÷ 12 base seven
Solution:
Step 1: Convert to base ten
For 2115 base seven
= 2 x 7³ + 1 x 7² + 1 x 7¹ + 5 x 7°
= 686 + 49 + 7 + 5
= 747 base ten
For 12 base seven
= 1 x 7¹ + 2 x 7°
= 7 + 2 = 9 base ten
Step 2: Now divide.
747/9 = 83 base ten
Step 3: Convert back to base seven.

83 base ten = 146 base seven.
So, (2115 ÷ 12) base ten = 146 base seven.
Example 5:
Divide 1423 by 24 in base five.
Solution:
Step 1: Convert to base ten
For 1423 base five
= 1 x 5³ + 4 x 5² + 2 x 5¹ + 3 x 5°
= 125 + 100 + 10 + 3
= 238 base ten
For 24 base five
= 2 x 5¹ + 4 x 5°
= 10 + 4 = 14 base ten
Step 2: Divide
238/14 = 17 base ten
Step 3: Convert back to base five

Therefore:
1423 base five ÷ 24 base five = 32 base five
OTHER CASES OF NUMBER BASES.
Number base sometimes have unknown that must be made known.
Example 1:
Calculate “y” if 134 base “y” = 54 base eight
Step 1: Convert both sides to base ten
For 134 base “y”
= 1 x y² + 3 x y¹ + 4 x y°
= (y² + 3y + 4) base ten
For 54 base eight
= 5 x 8¹ + 4 x 8°
= 40 + 4 = 44 base ten
Step 2: Equate the two terms.
(y² + 3y + 4) = 44
y² + 3y + 4 = 44
y² + 3y + 4 -44 = 0
y² + 3y – 40 = 0
Solving the quadratic equation
y² + 8y – 5y – 40 = 0
y(y + 8) – 5(y + 8) = 0
(y – 5)(y + 8) = 0
Either (y – 5) = 0
or (y + 8) = 0
When y – 5 = 0
y = 5
And when y + 8 = 0
y = – 8
Number base cannot take a negative value,
so y = 5.
Example 2:
If 251 base “b” = 100 base two, find the value of “b”.
Solution:
Similar thing we did in example 1 above will be done here too.
Step 1: Convert to base ten.
For 251 base “b”
= 2 x b² + 5 x b¹ + 1 x b°
= (2b² + 5b + 1) base ten
For 100 base two
= 1 x 2² + 0 x 2¹ + 0 x 2°
= 4 + 0 + 0 = 4 base ten
Equating both of them
(2b² + 5b + 1) = 4
2b² + 5b + 1 = 4
2b² + 5b + 1 – 4 = 0
2b² + 5b – 3 = 0
2b² + 6b – b – 3 = 0
2b(b + 3) – 1(b + 3) = 0
(2b – 1)(b + 3) = 0
So, either 2b – 1 = 0 or
b + 3 = 0
If 2b – 1 = 0
b = 1/2
And if b + 3 = 0
b = -3
Base cannot have negative sign, hence b = 1/2
QUESTIONS AND SOLUTIONS (Number Bases):
Q1. Evaluate 3112 base five X 34 base five.
Solution:
Step 1: Convert to base ten
For 3112 base five
= 3 x 5³ + 1 x 5² + 1 x 5¹ + 2 x 5°
= 375 + 25 + 5 + 2 = 407 base ten
For 34 base five
= 3 x 5¹ + 4 x 5°
= 15 + 4 = 19 base ten
Step 2: Multiply both
407 x 19 = 7733 base ten
Step 3: Convert back to base five

(3112 x 34) base five = 221413 base five
Q2. Divide 2173 by 16 in base nine
Solution:
Convert to base ten.
For 2173 base nine
= 2 x 9³ + 1 x 9² + 7 x 9¹ + 3 x 9°
= 1458 + 81 + 63 + 3
= 1605 base ten
For 16 base nine
= 1 x 9¹ + 6 x 9°
= 9 + 6 = 15 base ten
Divide the numbers
1605/15 = 107 base ten
Return to base nine

2173 base nine ÷ 16 base nine = 128 base nine.
Q3. 111 x 101 in base two
Solution:
Convert to base ten
For 111 base two
= 1 x 2² + 1 x 2¹ + 1 x 2°
= 4 + 2 + 1 = 7 base ten
For 101 base two
= 1 x 2² + 0 x 2¹ + 1 x 2°
= 4 + 0 + 1 = 5 base ten
Multiply the both
7 x 5 = 35 base ten
Return the number base ten to base two

111 x 101 in base two = 100011 base two
Q4. 3132 base eight + 6 base eight
Solution:
Convert to base ten
For 3132 base eight
= 3 x 8³ + 1 x 8² + 3 x 8¹ + 2 x 8°
= 1536 + 64 + 24 + 2
= 1626 base ten
For 6 base eight
= 6 x 8° = 6 base ten
Add the two numbers
1626 + 6 = 1632 base ten
Return it to base eight

3140 base eight.
Q5. If 25 x 14 = 374, find the number base used.
Solution:
Let the number base used be “y”
(25 base y) X (14 base y) = 374 base y
Convert all to base ten
For 25 base y
= 2 x y¹ + 5 x y°
= (2y + 5) base ten
For 14 base y
= 1 x y¹ + 4 x y°
= (y + 4) base ten
For 374 base y
= 3 x y² + 7 x y¹ + 4 x y°
= (3y² + 7y + 4) base ten
If (25 base y) X (14 base y) = 374 base y
Then,
(2y + 5)(y + 4) = 3y² + 7y + 4
Expand the equation
2y² + 8y + 5y + 20 = 3y² + 7y + 4
Collection of like terms
2y² – 3y² + 13y – 7y + 20 – 4 = 0
-y² + 6y + 16 = 0
y² – 6y – 16 = 0
y² – 8y + 2y – 16 = 0
y(y – 8) + 2(y – 8) = 0
(y + 2)(y – 8) = 0
y = – 2 or 8
Therefore y = 8
Q6. Given that 132 base five = P base six, find P.
Solution:
Convert to base ten
For 132 base five
= 1 x 5² + 3 x 5¹ + 2 x 5°
= 25 + 15 + 2
= 42 base ten
For P base six
= P x 6° = P base ten
Equating both sides
P = 42 base ten
Convert back to base six

P = 110 base six
Q7. If 244 base n = 1022 base four, find n.
Solution:
Convert to base ten
For 244 base n
= 2 x n² + 4 x n¹ + 4 x n °
= (2n² + 4n + 4) base ten
For 1022 base four
= 1 x 4³ + 0 x 4² + 2 x 4² + 2 x 4°
= 64 + 0 + 8 + 2
= 74 base ten
Equating both of them
(2n² + 4n + 4) = 74
2n² + 4n – 70 = 0
n² + 2n – 35 = 0
(n – 5)(n + 7) = 0
n = 5 or – 7
Therefore n = 5
because we do not have negative base
Q8. A number is written as 52 base x. Four times the number is written as 301 base x. What is x?
Solution:
A number = 52 base x
Four times the number = 4 X 52 base x = 301 base x
Convert to base ten
For 4
= 4 X x° = 4 base ten
For 52 base x
= 5 X x¹ + 2 X x°
= (5x + 2) base ten
For 301 base x
= 3 X x² + 0 X x¹ + 1 X x °
= 3x² + 0 + 1
= (3x² + 1) base ten
4(5x + 2) = 3x² + 1
20x + 8 = 3x² + 1
3x² – 20x – 7 = 0
Let us use quadratic formula to find the value of “x”
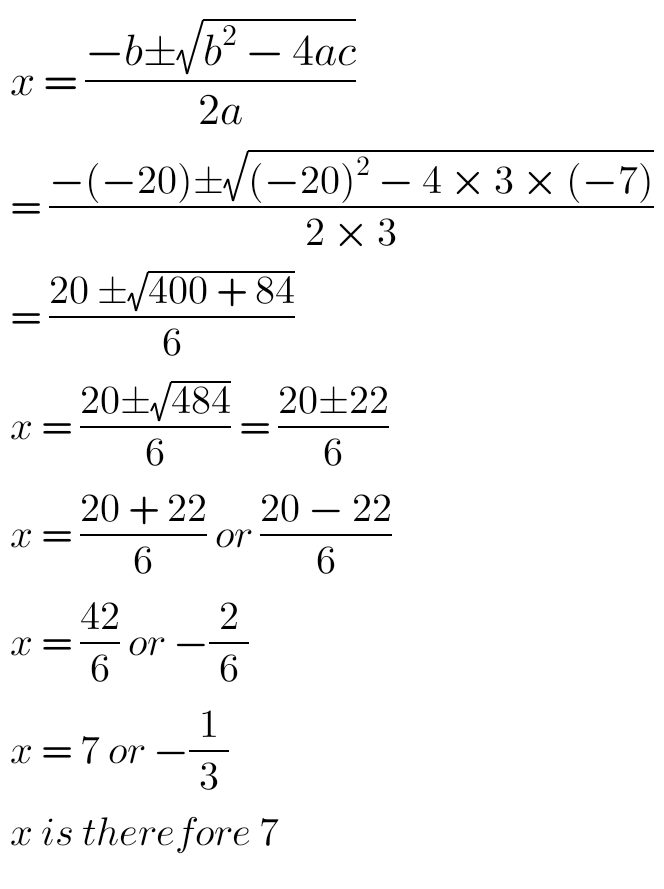
x = 7
Q9. Arrange the following in ascending order.
1101 base two, 26 base eight, 113 base four and 1024 base six.
Solution:
Convert all to base ten.
For 1101 base two
= 1 x 2³ + 1 x 2² + 0 x 2¹ + 1 x 2°
= 8 + 4 + 0 + 1
= 13 base ten
For 26 base eight
= 2 x 8¹ + 6 x 8°
= 16 + 6 = 22 base ten
For 113 base four
= 1 x 4² + 1 x 4¹ + 3 x 4°
= 16 + 4 + 3 = 23 base ten
For 1024 base six
= 1 x 6³ + 0 x 6² + 2 x 6¹ + 4 x 6°
= 216 + 0 + 12 + 4
= 232 base ten
Therefore, the ascending order of magnitude
= 1101, 26, 113 and 1024 to their respective bases.
Q10. If 321 base n = 232 base seven. Find the value of n.
Solution:
Convert all to base ten first.
For 321 base n
= 3 x n² + 2 x n¹ + 1 x n°
= (3n² + 2n + 1) base ten
For 232 base seven
= 2 x 7² + 3 x 7¹ + 2 x 7°
= 98 + 21 + 2
= 121 base ten
Equate the two.
3n² + 2n + 1 = 121
3n² + 2n + 1 – 121 = 0
3n² + 2n – 120 = 0
Using quadratic method to find the value of “n”
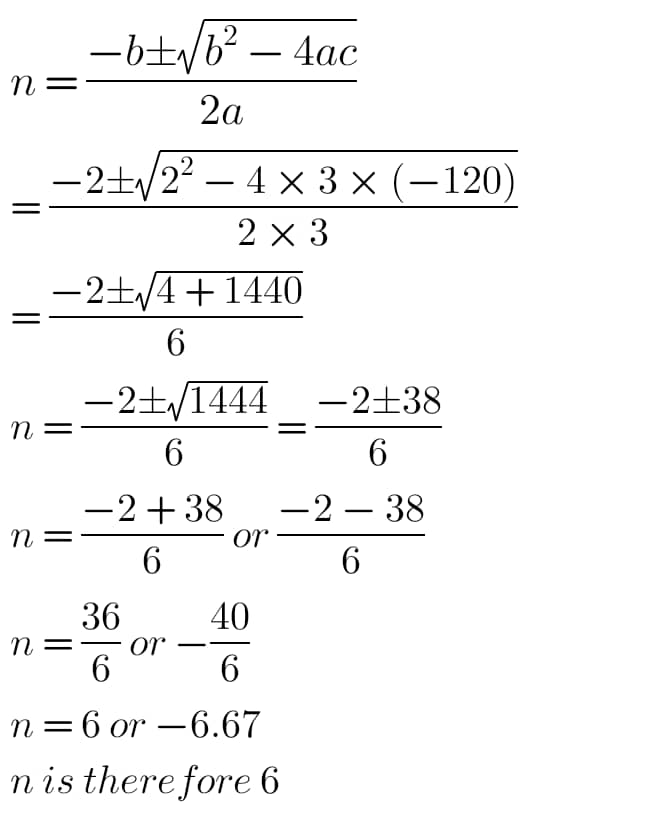
n = 6
Q11. Simplify the following binary numbers.
(a). 101 + 111
Solution:
Convert to base ten
For 101
= 1 x 2² + 0 x 2¹ + 1 x 2°
= 4 + 0 + 1 = 5 base ten
For 111
= 1 x 2² + 1 x 2¹ + 1 x 2°
= 4 + 2 + 1 = 7 base ten
101 + 111 = 5 base ten + 7 base ten
= 12 base ten
Convert 12 base ten back to binary.

Therefore 101 + 111 = 1100
(b). 11001 + 1111 + 10110
Solution:
For 11001
= 1 x 2⁴ + 1 x 2³ + 0 x 2² + 0 x 2¹ + 1 x 2°
= 16 + 8 + 0 + 0 + 1
= 25 base ten
For 1111
= 1 x 2³ + 1 x 2² + 1 x 2¹ + 1 x 2°
= 8 + 4 + 2 + 1
= 15 base ten
For 10110
= 1 x 2⁴ + 0 x 2³ + 1 x 2² + 1 x 2¹ + 0 x 2°
= 16 + 0 + 4 + 2 + 0
= 22 base ten
Add all
25 + 15 + 22 = 62 base ten
Convert it back to binary

Therefore 11001 + 1111 + 10110 = 111110
(c). 11111 – 1010
Solution:
For 11111
= 1 x 2⁴ + 1 x 2³ + 1 x 2² + 1 x 2¹ + 1 x 2°
= 16 + 8 + 4 + 2 + 1
= 31 base ten
For 1010
= 1 x 2³ + 0 x 2² + 1 x 2¹ + 0 x 2°
= 8 + 0 + 2 + 0
= 10 base ten
Subtract 10 base ten from 31 base ten
= 21 base ten.
Convert it back to binary
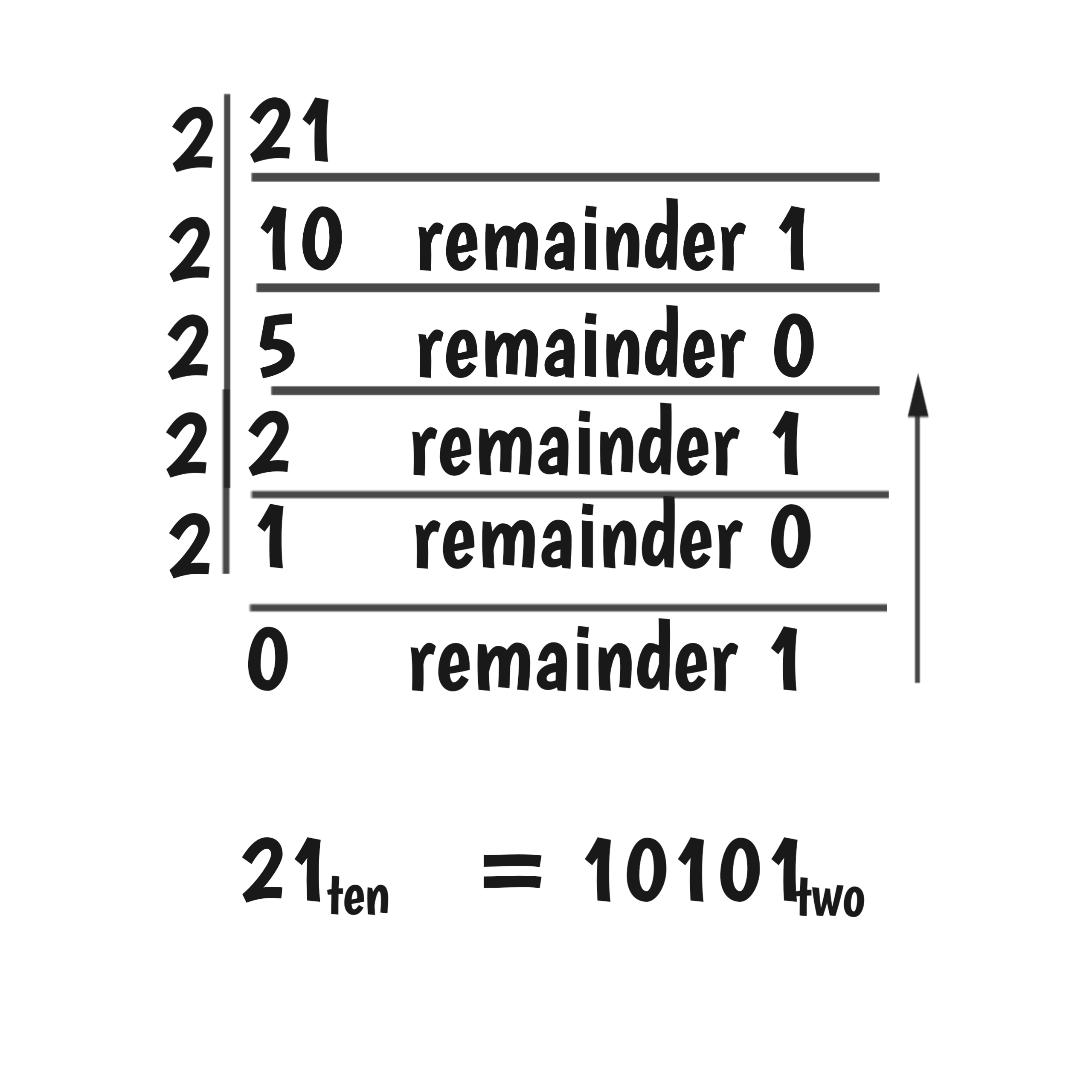
So, 11111 – 1010 = 10101
(d). 1111 x 110
Solution:
Convert both to base ten
For 1111
= 1 x 2³ + 1 x 2² + 1 x 2¹ + 1 x 2°
= 8 + 4 + 2 +1
= 15 base ten
For 110
= 1 x 2² + 1 x 2¹ + 0 x 2°
= 4 + 2 + 0
= 6 base ten
15 x 6 = 90 base ten
Return 90 base ten to binary

Thus, 1111 x 110 = 1011010
Q12. Simplify 342 base five + 134 base five + 223 base five and leave your answer in base
Solution:
Always convert to base ten first before any other thing.
For 342 base five
= 3 x 5² + 4 x 5¹ + 2 x 5°
= 75 + 20 + 2
= 97 base ten
For 134 base five
= 1 x 5² + 3 x 5¹ + 4 x 5°
= 25 + 15 + 4
= 44 base ten
For 223 base five
= 2 x 5² + 2 x 5¹ + 3 x 5°
= 50 + 10 + 3
= 63 base ten
Then, 97 + 44 – 63 = 78 base ten.
Convert 78 base ten to the required base, which is base five.

So, 342 base five + 134 base five + 223 base five = 303 base five.
Q13. Multiply (12012) base three by (201) base three.
Solution:
For 12012 base three
= 1 x 3⁴ + 2 x 3³ + 0 x 3² + 1 x 3¹ + 2 x 3°
= 81 + 54 + 0 + 3 + 2
= 140 base ten
For 201 base three
= 2 x 3² + 0 x 3¹ + 1 x 3°
= 18 + 0 + 1
= 19 base ten
140 by 19 = 140 x 19 = 2660 base ten
Convert the 2660 base ten back to base three.

Therefore, (12012) base three by (201) base three = 10122112 base three.
Q14. Divide (100001) base two by (11) base two
Solution:
Convert to base ten.
For 100001 base two
1 x 2^5 + 0 x 2⁴ + 0 x 2³ + 0 x 2² + 0 x 2¹ + 1 x 2°
= 32 + 0 + 0 + 0 + 0 + 1
= 33 base ten
For 11 base two
= 1 x 2¹ + 1 x 2°
= 2 + 1 = 3 base ten
Now divide
33 ÷ 3 = 11 base ten
Convert it back to base two.
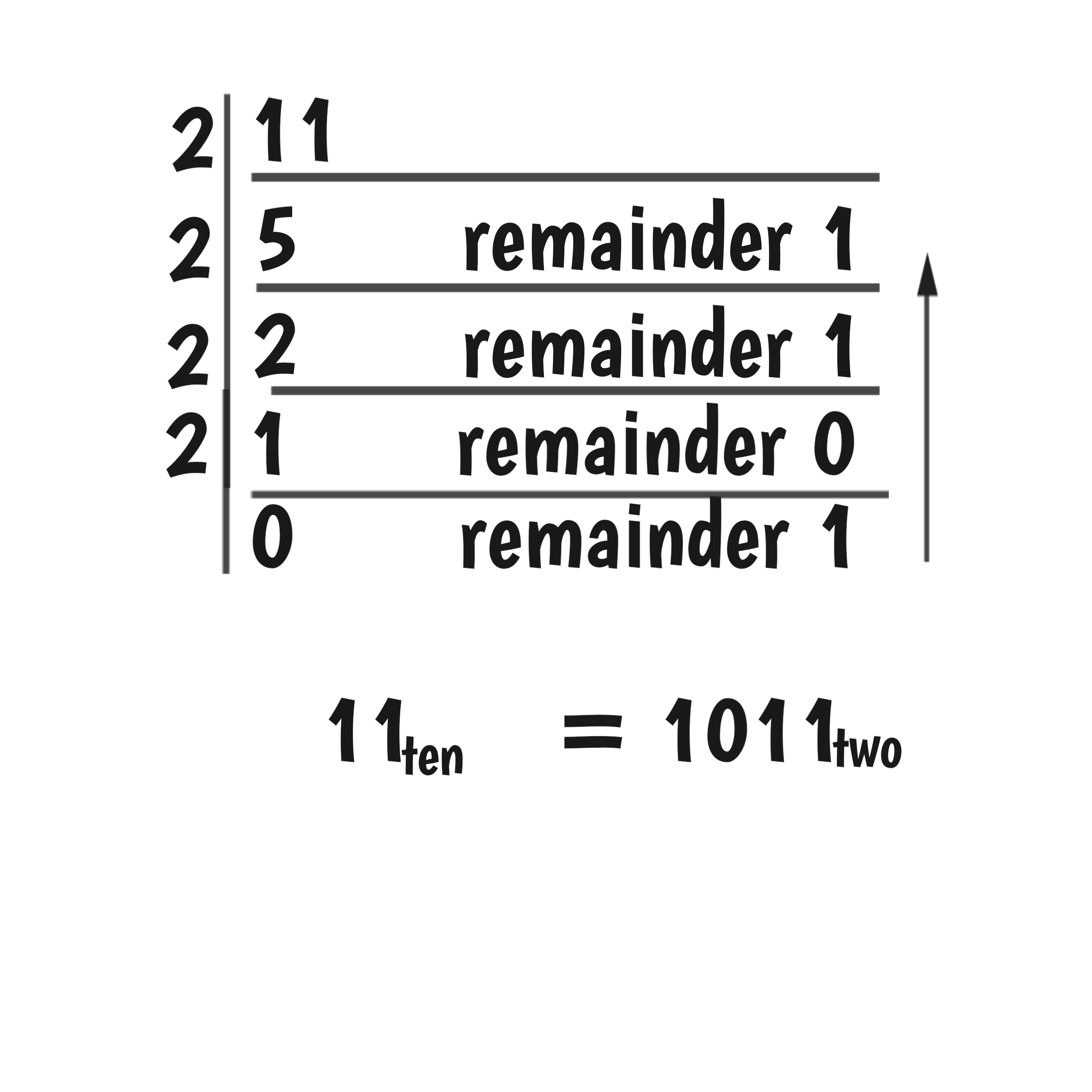
Therefore, 100001 base two divided by 11 base two = 1011 base two.