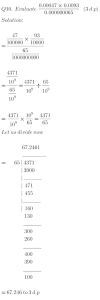How to add and subtract decimals

How to add and subtract decimals: When adding or subtracting decimal numbers, make sure you arrange the given decimal numbers in a column and the decimal points of each decimal number aligns with another down the column.

DECIMALS:

Decimal is equivalent to Fraction, it is another unique way of expressing Fractions.

Decimals are figures seen immediately after points and they are being pronounced “one” by “one”. What we mean here is that any figure, no matter how long it is, that you see immediately after decimal point are pronounced ONE by ONE. If for instance we have 59.425 , it is being pronounced “Fifty Nine” point “Four”— “Two”— “Five” and not “Fifty Nine” point “Four hundred and twenty five”.

0.789464 is pronounced “Zero” point “Seven”—”Eight”—”Nine”—”Four”—”Six”—”Four” and not “Zero” point “Seven hundred and eighty nine thousand, four hundred and sixty four”

DECIMAL PLACES (d.p)

For one to be able to determine the number of decimal places that a given figure contains, he/she should count the number of the digits from the LEFT to the RIGHT immediately after the decimal point.

Note: If zero(s) is/are among of the digits after the decimal point, it(the zero) will only be counted if it is found in between non zero digits and will not be counted if found at the last of the figure.

If we have three decimal numbers 0.0763539, 0.07635389, and 0.076353900, and you are asked to find their decimal places.

Solution:

Count the number of the digits from the left to the right immediately after the decimal point.

Note: Decimal Places is represented as (d.p)

Why is A and C giving us the same 7 d.p?.  This is because A and C have the same number of digits when counted from the left to the right immediately after the decimal point, the two zeros at the end of C will not be counted.

Example 1 (a). 2.40270653

I believe you know the reason why 2.40  = 1 d.p and not 2 d.p?. This is because the zero at the back of 2.4  is not counted.

(b). 0.007352

ADDITION AND SUBTRACTION OF DECIMALS

How to add and subtract decimals: When adding or subtracting decimal numbers, make sure you arrange the given decimal numbers in a column and the decimal points of each decimal number aligns with another down the column.

Example 1: (How to add and subtract decimals)

Add up 4.32, 3.761, 0.34, 3.6, 12.403

Solution:

Arrange the decimal numbers in one column.

Example 2: (How to add and subtract decimals)

Simplify 7.541 – 3.756

Solution:

Arrange the two decimal numbers in a column and making sure the decimal points align.

7.541

– 3.756

= 3.785

MULTIPLICATION OF DECIMALS.

There are actually three methods adopted in Multiplication of decimal which are:

1. Fraction or Standard form method: This is converting the decimal numbers to a known fraction first and multiply, which will now be converted back to decimal.

2. Assume the figures given are whole numbers which after Multiplying, will be converted back to the total of the places of decimal in the original figure.

3. This is the arrangement of the given figures in columns, in such a way that the first digit of the multiplier lies directly under the last digit of the one being multiplied(Multiplicand).

Example 1:

Simplify 3.75 x 4.65

Solution:

Using method 1.

Convert both to fractions.

When converting decimal to fraction;

first thing is to cross the given decimal number with a Division sign, thus creating a numerator and a denominator cell.

Second, the numerator should be the given number written as a whole.

Third; to get the denominator,  Call the very place that previously had a decimal point in the numerator ONE(1) and complete it with ZERO(s) depending on the number of digits in the numerator found immediately after  the decimal point.

Forth is to multiply the two fractions.

Now, convert the Standard form back to decimal number.

Using method 2:

Assume the figures as whole numbers.

Using method 3:

Any methods you use will give you the same answer.

DIVISION OF DECIMALS

Division of decimals is best done by first converting both the Dividend and the divisor to whole numbers before the division is being carried out.

Example 1:

Evaluate without using tables

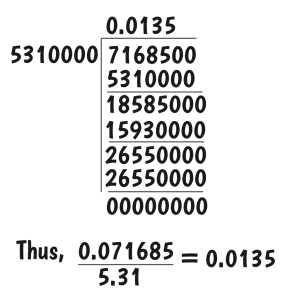
Let us now take some steps on how the division above is done.

Remember we have Dividend = 71685 and Divisor   = 5310000.

Step 1:

Form a Division table where, make a provision to enter the Divisor at the left, Dividend at the right and Quotient at the top.

Step 2:

Divide 71685 by 5310000, you will see that it will give you zero point and other digits (0.xxxx), write only the zero down at the place provided for quotient and put point(0.)

Step 3:

Add one zero to the dividend 71685, it will now be 716850, divide again as we did in step 2 above. You will still notice that the quotient is Zero point other digits, write only the zero again and leave those other digits(0.0).

Step 4:

Add another zero again to the present dividend 716850, it will now be 7168500, divide as we always have done before. If you divide now, it will give you ONE point other digits, write only the ONE down at the same quotient’s side and leave others(0.01).

Step 5:

Multiply the 1 gotten in step 4 above by the divisor, that is ( 1 x 5310000) = 5310000, write the product gotten directly under the divided.

Step 6:

Subtract the product from the dividend, that is: 7168500

Step 7:

Add zero to the result gotten from step 6 above = 18585000, divide it again by the divisor. If divided, it will give us THREE point other digit. Write only the THREE down at the quotient side(0.013), multiply that same THREE by the Divisor. 3 x 5310000 = 15930000

Step 8:

Write the 15930000 gotten in step 7 the way we have been doing and subtract it from 18585000 = 2655000.

Step 9:

Add zero to 2655000 = 26550000, divide by the divisor again = 26550000 ÷ 5310000 = 5, write it at the quotient side(0.0135), multiply by the divisor  again. 5 x 5310000 =  26550000.

Step 10:

Write the figure gotten from step 9 above under the column and subtract = 26550000 – 26550000 = 00000000. If you reach a juncture where the dividend is 0, you will know that the division has ended. Collect the quotient at the top and that is your answer in decimal.

QUESTIONS AND SOLUTIONS:

Q1 and Q2 and their Solutions: (How to add and subtract decimals)

Q3 and Q4 and their Solutions:

Q5 and its Solution

Q6 and its Solution

Q7 and Solution

Q8 and Solution

Q9 and Solution

Q10 and its Solution

Click here to see Mathematics past questions and answers